
Un árbol consta de un conjunto finito de elementos, llamados nodos y un conjunto limitado de líneas dirigidas, o ramas, que conectan a los nodos. La cantidad de ramas asociada con un nodo es el grado del nodo.
Si un árbol no está vacío, entonces el primer nodo se llama raíz.
- El nivel de un nodo es la distancia a la raíz.
- La raíz tiene una distancia cero de si misma, por lo que se dice que la raíz esta en el nivel 0.
- Los hijos de la raíz están en el nivel 1, sus hijos están en el nivel 2 y así sucesivamente.
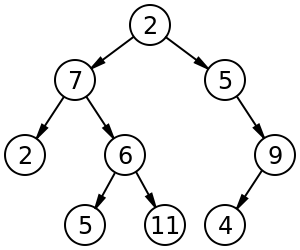
Árboles binarios
Un árbol binario es en el que ningún nodo puede tener mas de dos ramas (subárboles).
Cada nodo debe contener el campo dato y dos campos que señalen los subárboles (nodos) derecho e izquierdo.
La trayectoria de un árbol binario requiere que cada nodo del árbol sea procesado una vez y solo una en secuencia predeterminada.
Los recorridos se conocen como enorden, preorden y postorden.
Preorden (NID nodo-izquierdo-derecho):
Los pasos para el recorrido preorden es:
- Recorrer la raíz
- Recorrer el subárbol izquierdo en preorden
- Recorrer el subárbol derecho en preorden
Se visita primero la raíz, a continuación se visita el subárbol izquierdo, si el subárbol es también un árbol, se pasa por los nodos utilizando el orden NID
Enorden (izquierdo-nodo-derecho) IND:
El recorrido enorden procesa primero el subárbol izquierdo, después la raíz y a continuación el subárbol derecho. El método implica los siguientes pasos:
- Recorrer el subárbol izquierdo en inorden
- Visitar el nodo raíz
- Recorrer el subárbol derecho en inorden
Postorden (izquierdo-derecho-nodo) IDN:
El recorrido postorden procesa el nodo raíz después de que los subárboles izquierdo y derecho han sido procesados. Empieza situándose en la hoja mas a la izquierda y se procesa. A continuación se procesa su árbol derecho. Por último se procesa el nodo raíz. Etapas del algoritmo:
- Recorrer el árbol izquierdo en postorden
- Recorrer el árbol derecho en postorden
- Visitar el nodo raíz
Código
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 |
class nodo { int dato; nodo der; nodo izq; nodo(int dat) { this.dato=dat; this.der=null; this.izq=null; } } public class arbol { nodo raiz=null; public boolean tieneraiz() { if(raiz==null) return false; else return true; } public arbol alta(int dat) { if(!tieneraiz()) { nodo nuevo=new nodo(dat); raiz=nuevo; } else { boolean izq; nodo actual=raiz; while(true) { if(actual.dato<dat) izq=false; else izq=true; if(!izq) { if(actual.der==null) { nodo nuevo=new nodo(dat); actual.der=nuevo; break; } else actual=actual.der; } else { if(actual.izq==null) { nodo nuevo=new nodo(dat); actual.izq=nuevo; break; } else actual=actual.izq; } } }return this; } public boolean baja(int dat) { nodo actual=raiz, anterior=raiz, temp; while(true) { if(actual==null) break; if(actual.dato==dat) break; anterior=actual; if(actual.dato<dat) actual=actual.der; else actual=actual.der; } if(actual==null) return false; else { if(actual==raiz) { temp=actual.izq; raiz=raiz.der; anterior=raiz; } else if (anterior.der == actual) { temp=actual.izq; anterior=actual.der; } else { temp=actual.izq; anterior.der=actual.izq; } actual=new nodo(); while(actual.izq!=null) actual=actual.izq; actual.izq=temp; return true; } } public void imprimirpreorden() { ayudantePreorden(raiz); } public void ayudantePreorden(nodo dat) { if(dat==null) return; System.out.printf("%d ",dat.dato); ayudantePreorden(dat.der); ayudantePreorden(dat.izq); } public void impririnorden(nodo dat) { if(dat!=null) { impririnorden(dat.izq); System.out.println(" "+dat.dato); impririnorden(dat.der); } } } |





















Edgar González liked this on Facebook.
Arthur Van Wolfenstein liked this on Facebook.
jejejeje esos arboles son la onda cuando necesitas hacer variaciones de palabras y asi sacas todas las combinaciones posibles 🙂
Ivette Alvrz liked this on Facebook.
Adriana Lizette Ramírez de Uribe liked this on Facebook.
Marcela Sena liked this on Facebook.
Liz Loera liked this on Facebook.
David Bonilla liked this on Facebook.
Jaan Snow liked this on Facebook.
Oscar Alfredo Flores Solano liked this on Facebook.
Luis Angel Gomez Velazco liked this on Facebook.
Que buen quick-refresh para mi entrevista xD