El estándar IEEE 754
Esta norma surge por los años 1985 estandarizando la forma de realizar las operaciones aritméticas y la forma de representar los números en punto flotante por el Instituto de Ingenieros Eléctricos y Electrónicos (IEEE).
Siempre ha sido un dolor de cabeza para todos aquellos estudiantes de informática en algún punto de sus vidas.
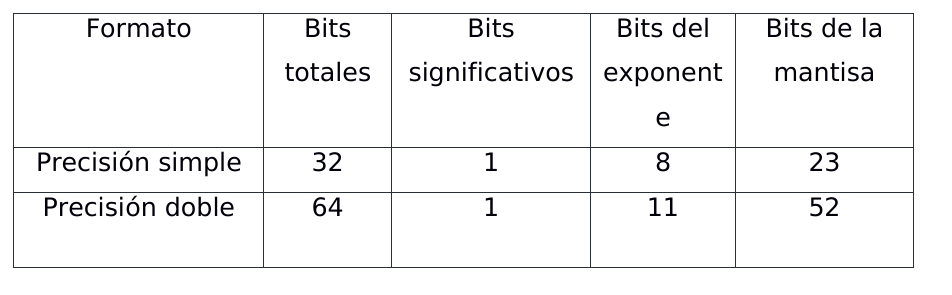
Como ya sabemos hay diferentes tipos de arquitecturas en las computadoras, de los más conocidos son los de 32 y 64 bits, los cuales hacen referencia al tipo de unidad central de proceso (CPU). Los componentes de las computadoras deben de ser de la misma arquitectura para que puedan comunicarse entre ellos sin problemas. Pero… ¿A que viene todo esto?, bueno, en nuestro caso nos importa la manera en como almacena los datos. ¿Por qué? Porque la memoria es limitada, no se pueden almacenar números con precisión infinita, para lo cual se debe cortarlo en pedazos.
Existen dos formatos para representar a los números reales:
- Precisión simple.
- Precisión doble.
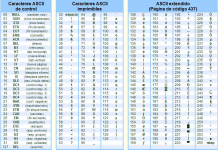
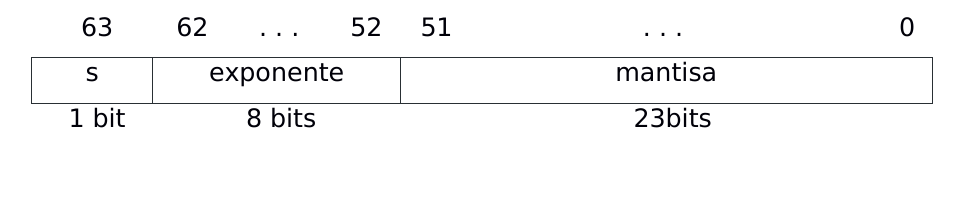
Tomando como ejemplo esta imagen podremos ver que el número se divide en 3 partes:
- Bit significativo (0/1) que nos dice si es positivo o negativo el número.
- El exponente que nos indica dónde se coloca el punto decimal (o binario) en relación al inicio de la mantisa.
- Una mantisa (también llamada coeficiente o significando) que contiene los dígitos del número.
Precisión simple
Precisión doble
¿Por qué cuando sumas números decimales no son exactos?
Algunos lenguajes de programación tienen problemas de precisión como por ejemplo: java, python, javascript, c++. También hay algunos que no, como es el caso de C.
Los lenguajes que tienen problemas de precisión cuando se hacen operaciones con decimales. ¿Cómo es esto? Pues sí, es sencillo, a veces realizamos operaciones y esperamos un número exacto como 0.04 o 0.02 pero en realidad lo que obtenemos es 0.09000000000000001 y este problema no solo afecta Javascript sino a la mayoría de los lenguajes.
Veamos un ejemplo.
|
1 2 3 4 5 6 |
function example() { let x = 0.2 + 0.1; console.log('x: ', x); } example(); // x: 0.30000000000000004 |
La razón por la cual no nos esta devolviendo el resultado deseado esta fuertemente relacionado con la forma en la que se representan los números decimales en las computadoras.
Creemos que tiene error y la verdad es que no, internamente funciona diferente ya que solo contamos con 1’s y 0’s (binario).
¿Cómo resolver el problema de precisión de decimales en Javascript?
Este es un problema muy común y existen diferentes maneras de resolverlo.
Vamos a hacer referencia de alguna de ellas:
- Si solo quiere eliminar los decimales extras: puede hacerlo redondeando su resultado a un número fijo.
- Si sus calculos deben ser muy exactos por que esta manejando con dinero lo más recomendable es usar un tipo de dato decimal especial.
- Otra alternativa es trabajar con solo enteros.
En este caso ya que hablamos más enfocados en el lenguaje Javascript y necesitas calculos exactos te recomendamos usar BigDecimal que resuelve el problema.
Usando BigDecimal podríamos hacer lo siguiente:
|
1 2 3 4 5 6 7 |
let amount1 = new Big(“0.1”); let amount2 = new Big(“0.2”); let result = amount1.plus(amount2); console.log('result: ', result); // result: 0.3 |
Con eso vemos que el problema de exactitud ha sido resuelto.
